🔑【数据结构】之查找

排序

基本概念

排序

将原本无序的序列重新排列成有序序列的过程

稳定性

当排序序列当中有两个或两个以上相同的关键字时，排序前后这些关键字的相对位置不变

排序算法的分类

1. 插入类排序
   直接插入排序、折半插入排序、希尔排序
2. 交换类排序
   冒泡排序、快速排序
3. 选择类排序
   简单选择排序、堆排序
4. 归并类排序
   二路归并排序
5. 基数类排序
   多关键字排序

插入类排序

直接插入排序

算法思想：每趟将一个待排序的关键字按照其值得大小插入到已经排好的部分有序序列的适当位置上，直到所有关键字全部插入为止

算法图解：

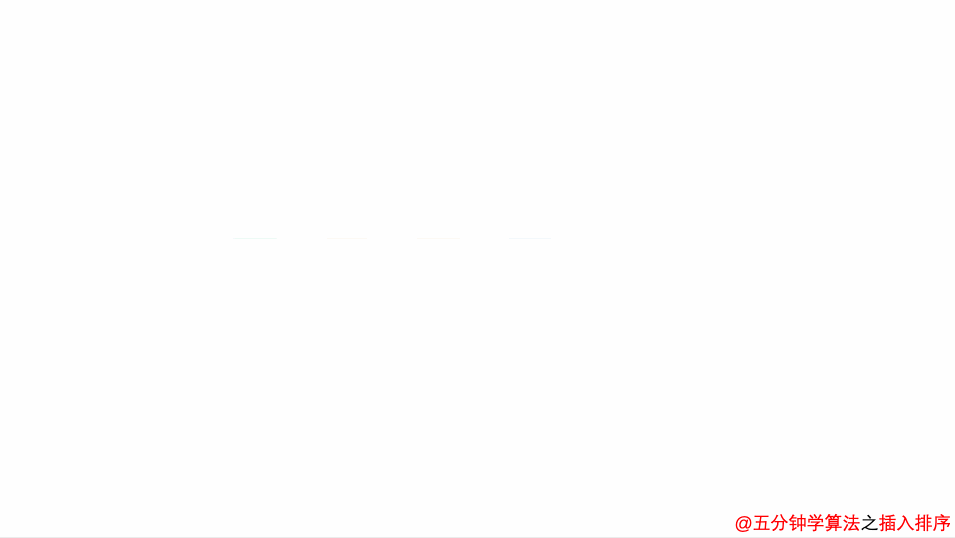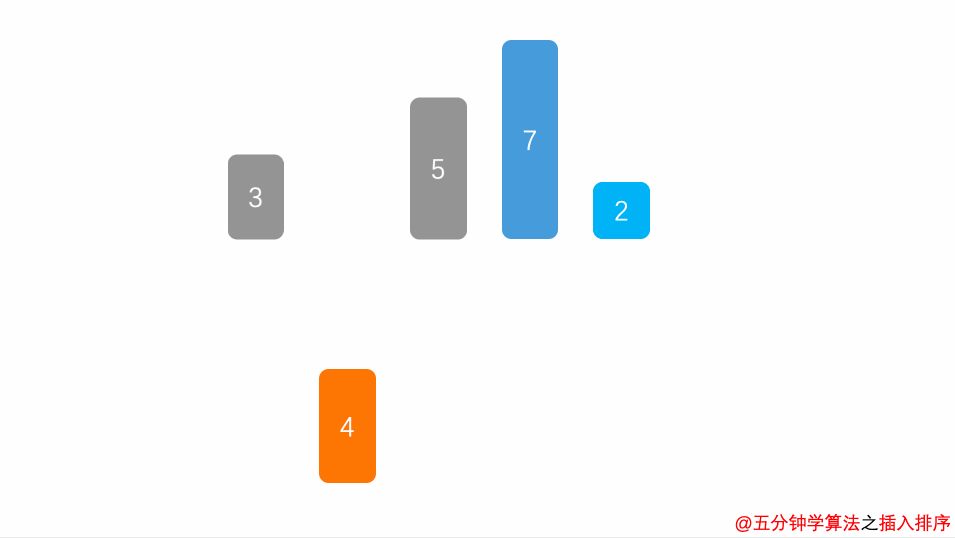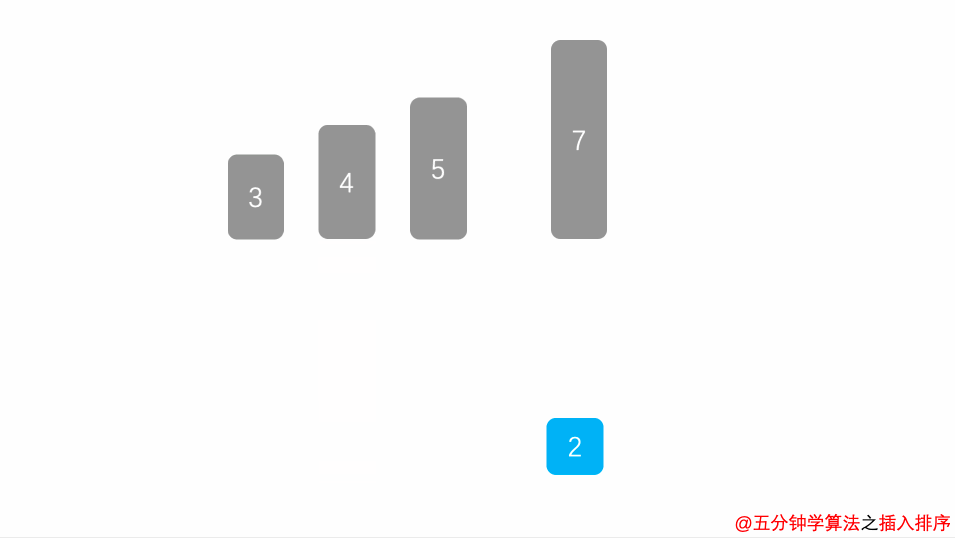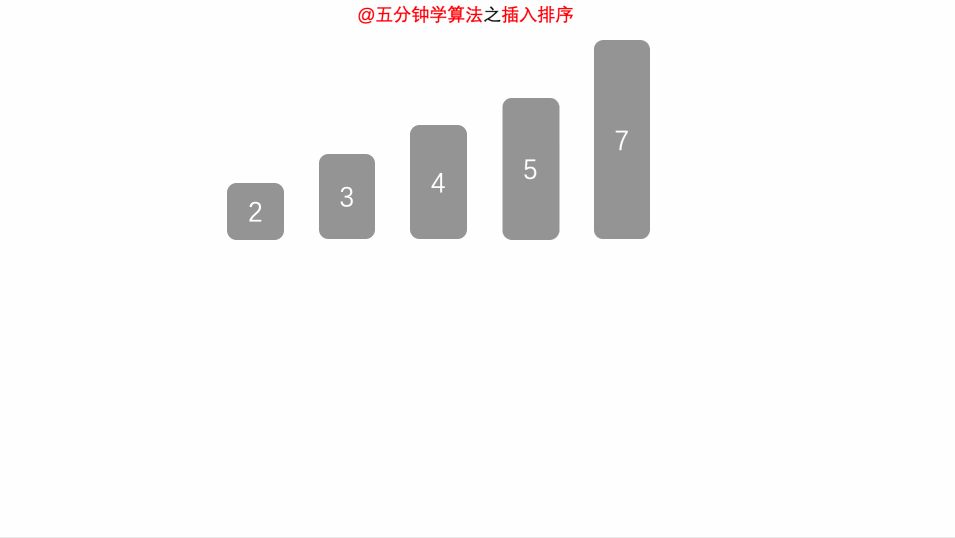
void InsertSort(int R[],int n)
{
    int i,j;
    int temp;
    for(i=1;i<n;++i)
    {
        temp=R[i];
        j=i-1;
        while(j>=0&&temp<R[j]) //注意：每次比较都是和之前的元素比较，不符合条件再继续向前比较
        {
            R[j+1]=R[j];
            --j;
        }
        R[j]=temp;
    }
}

算法性能

• 时间复杂度：最坏：$O(n^2)$，最好：$O(n)$，平均：$O(n^2)$
• 空间复杂度：辅助空间是常量，$O(1)$
  最坏的情况：整个序列都是逆序
  最好的情况：整个序列都是有序

折半插入排序

算法思想：每次在有序序列当中插入关键字，插入位置用折半查找法
算法性能：

• 时间复杂度：最好$nlog_2n$,最差$O(n^2)$，平均$O(n^2)$
• 空间复杂度：$O(1)$

希尔排序（缩小增量排序）

算法思想：以增量分割序列，进行直接插入排序，逐步缩小增量，例：5，3，1（希尔排序不稳定）

算法图解：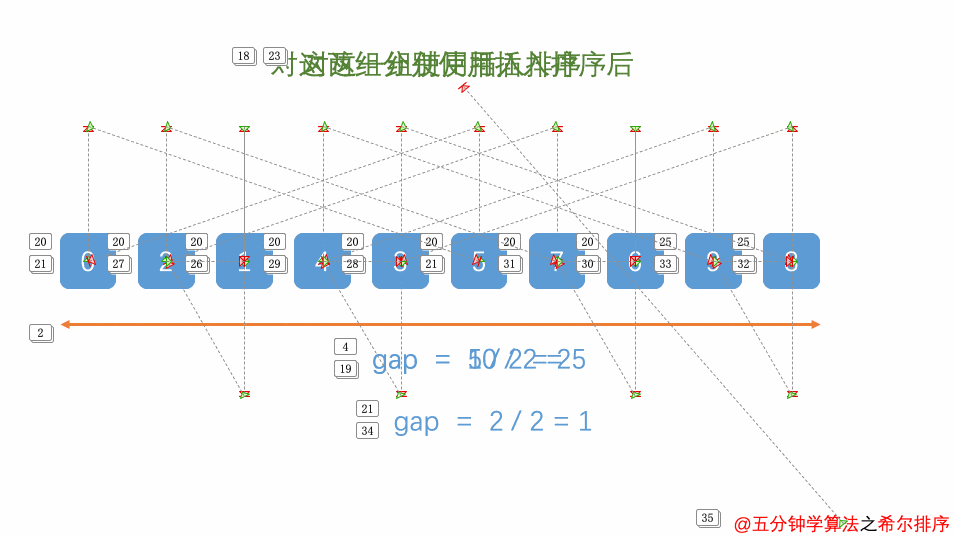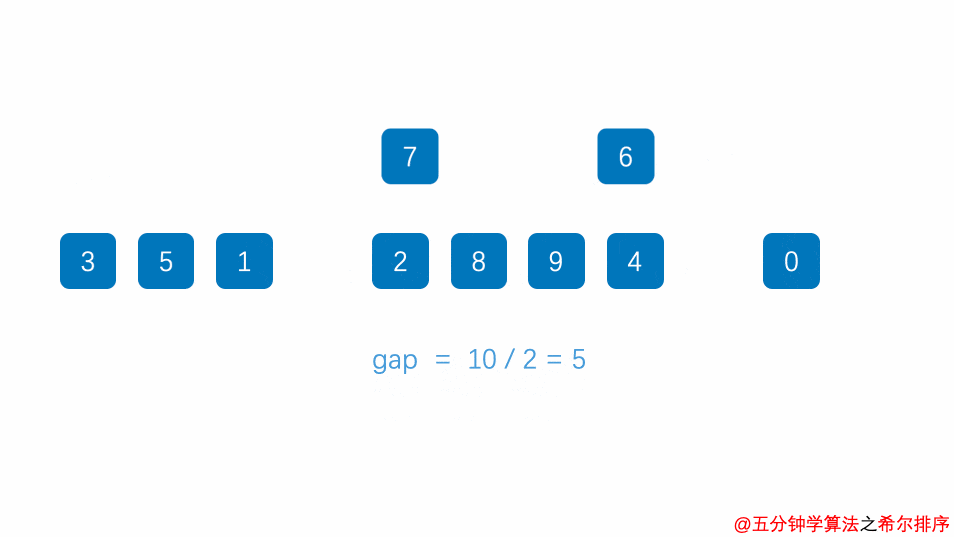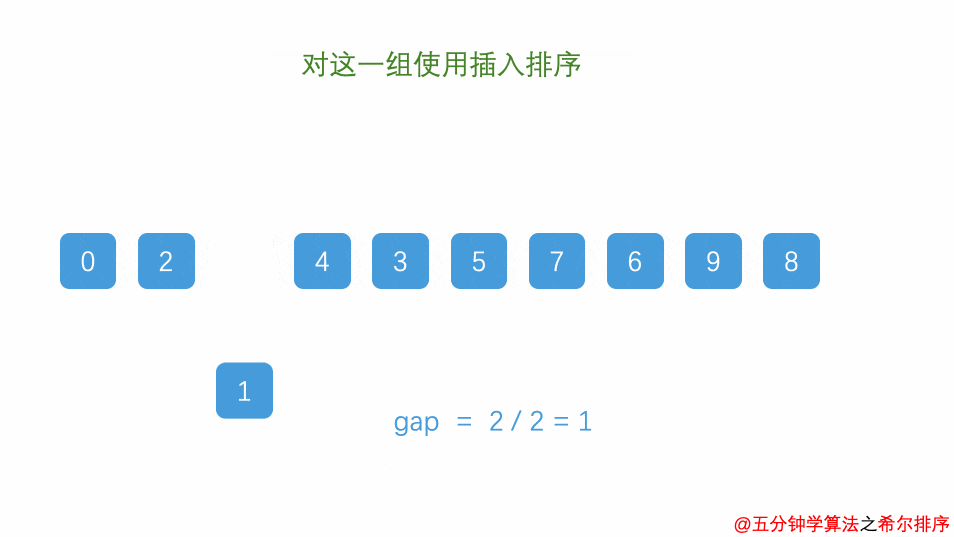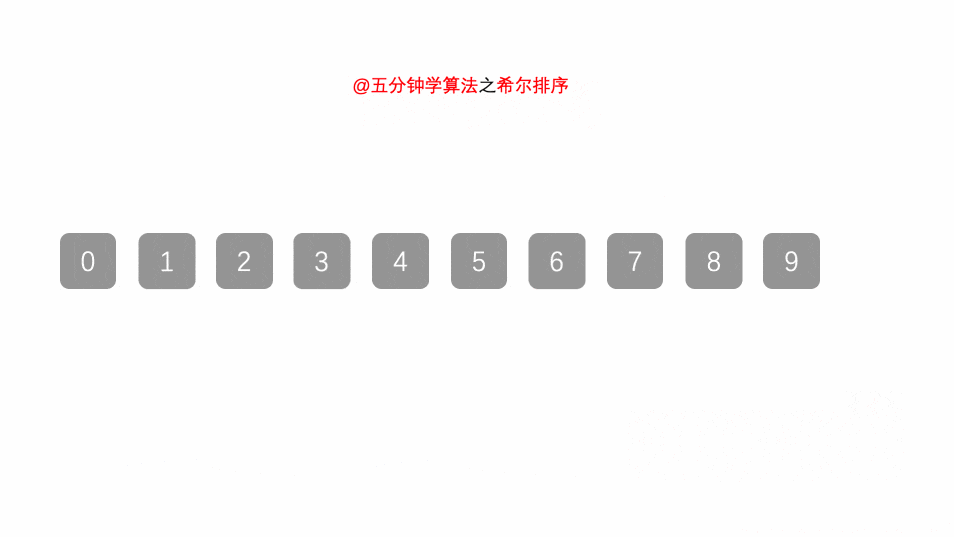

算法性能：

• 增量选取规则：
  • 希尔自己提出：$n/2^k$（k指次数），此时时间复杂度为：$O(n^2)$
  • 怕佩尔诺夫和斯塔舍维奇：$2^k+1$ （k为大于1的整数，$2^k+1$小于n，此时时间复杂度为$O(n^{1.5})$
  • 空间复杂度：$O(1)$

注意：增量序列的最后一个值一定取1，增量序列中的值尽量没有除1以外的公因子

交换类排序

冒泡排序

算法思想：略

算法图解：

void BubbleSort(int R[],int n)
{
    int i,j,flag;  int temp;
    for(i=n-1;i>=1;--i)
    {
        flag=0;
        for(j=1;j<=i;j++)
        {
            if(R[j-1]>R[j])
            {
                temp=R[j];
                R[j]=R[j-1];
                R[j-1]=temp;
                flag=1;
            }
            if(flag==0)
            return;
        }

    }
}

算法性能：
时间复杂度：好：$O(n)$;坏：$O(n^2)$,平均$O(n^2)$
空间复杂度：$O(1)$

快速排序

算法思想：每次把第一个当做关键字，比关键字小的放在关键字之前，比关键字大的放在关键字之后

算法图解：

void QuickSort(int R[],int low,int high)
{
    int temp;
    int i=low,j=high;
    if(low<high)
    {
        temp=R[low];
        while(i<j)
        {
            while(i<j&&R[j]>=temp) --j;
            if(i<j)
            {
                R[i]=R[j];
                ++i;
            }
            while(i<j&&R[i]<temp) ++i;
            if(i<j)
            {
                R[j]=R[i];
                --j;
            }
        }
        R[i]=temp;
        QuickSort(R,low,i-1);
        QuickSort(R,i+1,high);
    }
}

算法性能：
时间复杂度：最好：$O(nlog_2n)$,最差:$O(n^2)$,平均:$O(nlog_2n)$
空间复杂度：$O(log_2n)$,递归进行，需要栈的辅助

选择类排序

简单选择排序

算法思想：从头至尾扫描序列，找出最小的和第一个关键字交换，直到最后，使序列有序

算法图解：

void SelectSort(int R[],int n)
{
    int i,j;
    int temp;
    for(i=0;i<n;++i)
    {
        for(j=i+1;j<n;++j)
        {
            if(R[i]>R[j])
            temp=R[i];
            R[i]=R[j];
            R[j]=temp;
        }
    }
}

算法性能：
时间复杂度：$O(n^2)$
空间复杂度：$O(1)$

堆排序

算法思想：把堆看成一颗完全二叉树，满足：任何一个非叶子结点的值都不大于（或不小于）其左右孩子结点的值，若父亲大孩子小，叫大顶堆，若父亲小孩子大，叫小顶堆。

执行步骤：

1. 按层建立二叉树
2. 按照自下而上，自左到右比较调整
3. 插入结点：放在最底层最右边（满足完全二叉树的特点），再调整位置
4. 删除结点：把最底层最右边的值赋给删除的位置，并下调到合适的位置，然后把该结点删除
5. 排序：去除根节点，在将其重新调整为大顶堆

算法图解：

算法性能：
时间复杂度：$O(nlog_2n))$
时间复杂度：$O(1)$

二路归并排序

算法思想：两两归并，形成二元组，排序后，继续两两归并，形成四元组，在进行归并，直至有序

算法图例：

算法性能：
时间复杂度：$O(nlog_2n)$
空间复杂度：$O(n)$

基数排序

算法思想：多关键字排序，分为高位优先（按最高位排列，再对子列按次高位排列）和低位优先（桶先进先出）

算法图例：

算法性能：
时间复杂度：$O(d(n+r_d))$
空间复杂度：$O(r_d)$
（n为关键字数，d为关键字位数，$r_d$为关键字基的个数（桶的个数））

知识点总结

• 复杂度
  • 时间：快些归队（快速、希尔、归并、堆）$O(nlog_2n)$，其余都是$O(n^2)$
  • 空间：快排$O(log_2n)$，归并$O(n)$，基数$O(r_d)$,其他都是$O(1)$
• 稳定性：情绪不稳定，快些选一堆朋友聊天（快排、希尔、选择、堆排序）不稳定
• 其他
  • 每次都能保证一个关键字到达最终位置，属于交换类和选择类
  • 关键字比较次数和原始序列无关，简单选择排序和折半插入排序
  • 排序趟数和原始序列有关，交换类排序
  • 借助比较进行排序的算法，最坏的时间复杂度至少为$O(nlog_2n)$